Analytic Models for Computer Architecture

From the smallest embedded system to the largest warehouse-scale computing infrastructure, from the most well-characterized CMOS technology node to novel devices at the edge of our understanding, computer architects are expected to be able to speak to concerns of energy, cost, leakage, cooling, complexity, area, power, yield, and of course performance of a set of designs.  Even radical approaches such as DNA-based computing and quantum architectures are to be considered.  While careful application of detailed simulation can accurately estimate the potential of a specific microarchitecture, exploration across higher level questions always involves some analytic models.  

For example, ``given some target cooling budget, how much more performance can I get out of an ASIC versus an FGPA for this application given my ASIC will be 2 tech nodes behind the FPGA?'' The explosion of domain-targeted computing solutions means that more and more people are being asked to answer these questions accurately and with some understanding of the confidence in those answers.  While any Ph.D. in Computer Architecture should be able to answer this question, when you break it down, it requires a combination of a surprisingly complex set of assumptions.  How do tech node and performance relate?  What is the relationship between energy use and performance? ASIC and FPGA performance? Dynamic and leakage power? Temperature and leakage?  Any result computed from these relationships will rely on the specific relationships chosen, on those relationships being accurate in the range of evaluation, on a sufficient number of assumptions being made to produce an answer (either implicitly or explicitly), and finally on that the end result be executable to the degree necessary to explore a set of options (such as for a varying parameter e.g., total cooling budget). 

What is Charm?

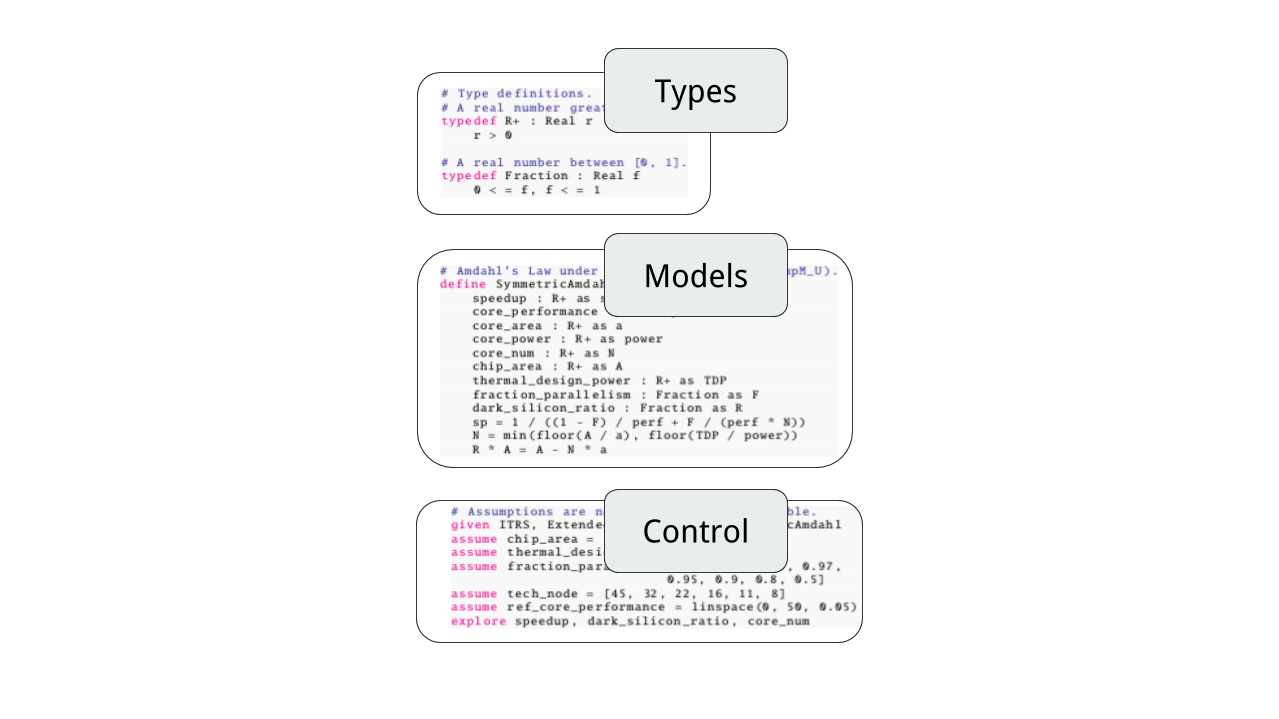
Charm is a modeling language that provides a concise and natural way to express architectural relationships and declare analysis goals. By combining symbolic manipulation, constraint solving, and compiler techniques, Charm bridges the gap between mathematical equations and executable, optimized evaluation functions and analysis procedures.

Clean Abstraction

Charm encapsulates a set of mutually dependent relationships and supports flexible function generation. It enables representation of architecture models in a mathematically consistent way. Depending on which metric the model is trying to evaluate, Charm can generate corresponding functions without requiring the user to re-write the equations. It also modulates high-level architecture models by packing commonly used equations, constraints and assumptions in modules. These architectural ``rules of thumb'' can then be easily composed, reused and extended in a variety of modelling scenarios.

Model Consistency Checking

Charm enables new static and run-time checking capabilities on high-level architecture models by enforcing a type system in such models. One example is that many architecturally meaningful variables have inherent physical bounds that they must satisfy; otherwise, although mathematically viable, the solution is not reasonable from an architectural point of view. With the type system built-in, Charm can dynamically check if all variables are within defined bounds to ensure a meaningful modelling result. The type system also helps prune the design space based on constraints, without which a declarative analysis might end up wasting a huge amount of computing effort in less meaningful sub-spaces.

Composition and Optimization

Charm automatically manages multiple "instances" of sets of equations that naturally occur in architecture models.  It further opens up new opportunities for compiler-level optimization when evaluating architecture models. Although high-level architecture models are usually several orders of magnitude faster than detailed simulations, as the model gets complicated or is applied many times to estimate a distribution, it can still take a non-trivial amount of time to naively evaluate the set of equations every iteration.  By expressing these complicated models in Charm, we are able to identify common intermediate results to hoist outside of the main design option iteration and/or apply memoization on functions.

Exploring Architectural Risk using Charm

Designing a system in an era of rapidly evolving application behaviors and significant technology shifts involves taking on risk that a design will fail to meet its performance goals. While risk assessment and management are expected in both business and investment, these aspects are typically treated as independent to questions of performance and efficiency in architecture analysis. As hardware and software characteristics become uncertain (i.e. samples from a distribution), we demonstrate that the resulting performance distributions quickly grow beyond our ability to reason about with intuition alone. We further show that knowledge of the performance distribution can be used to significantly improve both the average case performance and minimize the risk of under-performance (which we term architectural risk).  Charm can be used to quantify the areas where trade-offs between expected performance and the ``tail'' of performance are most acute and provide new insights supporting architectural decision making (such as core selection) under uncertainty.